Écriture d'un entier dans différentes bases

Problématique

Questions diverses

Voici quelques questions auxquelles nous répondrons dans ce chapitre :

• comment puis-je compter jusqu’à 1023 avec mes deux mains ?
• que signifie cette plaisanterie célèbre dans le monde des geeks : "Dans le monde il y a 10 types de personnes, celles qui comprennent le binaire, et les autres" ?
• pourquoi 123 peut aussi s’écrire 173 ?

Le codage des informations

Vous le savez sans doute mais les ordinateurs ne savent manipuler que des 0 et des 1.

Autrement dit, toutes les images, vidéos et textes que vous trouvez sur Internet ou sur votre disque dur n'existent que sous cette forme du point de vue de la machine.

Prenons le cas d'un texte : un texte est une suite de caractères, à chaque caractère correspond un nombre (par exemple, le "A" est associé à 65 dans le code ASCII) donc un texte est une suite de nombres, qu'il suffit ensuite de convertir en séries de 0 et de 1.

C'est ce dernier point que nous allons traiter dans ce chapitre : la conversion d'un nombre entier en série de 0 et de 1 (et réciproquement), autrement dit en binaire, ainsi que l'écriture hexadécimal.

L'écriture binaire

Principe

Exercice

Préparation

Disposez les cinq cartes que vous avez reçues sur la table en face de vous en respectant l’ordre (à conserver tout le temps) ci-dessous :

(si vous n'avez pas reçu ces cartes, fabriquez-en...).

Phase 1

• comment passe-t-on du nombre de points d'une carte à celui figurant sur celle qui est à sa gauche ? sous quelle forme commune pouvons-nous écrire chacun des nombres de points ?
• demandez à votre binôme de choisir un entier au hasard (exemples : 6 ; 7 ; 15...) ; retournez ou ne retournez pas certaines cartes de façon à compter autant de points visibles que le nombre entier choisi ;
• maintenant inversez les rôles, et demandez à votre binôme d’afficher un autre entier que vous avez choisi au hasard...
• existe-t-il un nombre qui peut être représenté de deux façons différentes avec les cartes ?
• peut-on afficher n'importe quel entier ?
• quel est le plus petit entier représentable ? quel est le plus grand ?
• à l'aide des cartes, comptez à partir de 0 et essayez de repérer le mécanisme de progression...

Phase 2

Pour chaque carte : je note 1 si elle est tournée du côté qui comporte des points et 0 sinon.

Ainsi, pour le nombre 21 = 16 + 4 + 1 :

J'obtiens ainsi un mot de 5 bits (5 chiffres choisis parmi 0 et 1).

Quel nombre est représenté par le mot 01001 ?

Quel nombre est représenté par le mot 00000 ?

Quel nombre est représenté par le mot 11111 ? Comment le calculer rapidement ?

Sauriez-vous écrire 17 en binaire ?

Si vous avez fini ce qui précède, essayez de convertir d'autres entiers en binaire et demandez à votre binôme de retrouver l'entier initial...

Enfin, faîtes l'exercice 1 de la fiche d'exercices.

À retenir

Le système binaire est un système de numération (d'écriture de nombres) de position de base deux : les deux seuls chiffres qui le composent sont le 0 et le 1.

Un chiffre binaire est appelé bit (contraction de binary digit). Un bit ne peut avoir que deux états : 0 ou 1.

Avec n bits, je peux représenter les nombres entiers de 0 à 2ⁿ-1, ce qui fait 2ⁿ entiers.

Les informations sont souvents découpées en mots de 8 bits ou octet. Par exemple 01100010 est un octet.

Un byte est maintenant synonyme d'un octet (cela n'a pas toujours été le cas). Attention à ne pas confondre un byte et un bit (exemple : 1 kB = 8 kb) !

Voici les deux écritures des dix premiers entiers :

Décimal	0	1	2	3	4	5	6	7	8	9
Binaire	0	1	10	11	100	101	110	111	1000	1001

(remarque : 0 et 1 s'écrivent toujours de la même façon dans tous les systèmes).

Qu'est ce qu'un chiffre ?

Un chiffre n'est pas un nombre (sauf les chiffres d'affaires...).

De la même façon que les mots s'écrivent avec des lettres et qu'en français nous n'avons que 26 lettres qui permettent d'écrire beaucoup de mots, les nombres s'écrivent avec des chiffres et nous n'utilisons que 10 chiffres (10 symboles : 0, 1, 2, ..., 9) qui nous sont bien familiers mais qui sont néanmoins artificiels. Ces symboles sont apparus progressivement dans les écrits indiens puis repris dans les textes arabes et enfin transmis en Europe via l'Italie.

Donc dans notre système habituel (le système décimal) nous avons besoin de 10 symboles pour écrire des nombres tandis qu'en binaire il en suffit de 2 : les chiffres 0 et 1.

Exercice

Regardez cette vidéo.

MSB et LSB

L'acronyme M.S.B. signifie "most significant bit", il désigne le bit le plus à gauche, on dit aussi bit de poids le plus fort.

Le bit de poids le plus faible (situé le plus à droite) est appelé L.S.B. (less significant bit ).

Exercice

Phase 3

Combien existe-t-il d'octets différents ? ...

Avec un octet je peux coder des nombres entiers allant de ... à ...

Combien d'octets ont un MSB égal à 1 ? ...

Comment peut-on compter jusqu'à 1023 avec dix doigts ? Réfléchissez puis si vous n'avez pas trouvé, vous pouvez regarder cette vidéo.

Source

Eric MADEC et Y. Moncheaux

Addition en binaire

Exercice

Faîtes l'addition 1 + 1 :

• en décimal ;
• en binaire.

Explications

Eh oui, en binaire 1 + 1 = 10 !

Retenez que :
0 + 0 = 0
1 + 0 = 0 + 1 = 1
1 + 1 = 10, autrement dit je place un zéro et je mets une retenue de 1 sur le bit qui suit à gauche.

Exercice

Exercice 2 de la fiche d'exercices, question 1°).

Multiplication en binaire

Les tables de multiplication en binaire se résument à ceci :
0 × 0 = 0 ; 0 × 1 = 1 × 0 = 0 ; 1 × 1 = 1.
Par exemple, calculons 1011 × 11001 (en décimal : 11 × 25 = 275).
La multiplication se fait de façon usuelle, en n'oubliant pas le décalage (zéro à droite, en rouge ci-dessous) à chaque ligne, le résultat final s'obtient par addition.

1011
× 1 1 0 0 1
1011
00000
000000
1011000
10110000
= 100010011

(en décimal : 275).

Si vous n'avez pas encore bien compris, vous pouvez regarder cette vidéo.

Exercice

Exercice 2 de la fiche d'exercices, question 2°).

Notations

Les nombres entiers peuvent donc s'écrire sous différentes formes.

Mais que représente l'écriture 101 par exemple ? Est-ce "cent un" ou 4 + 1 = 5 ?

Il faut donc préciser quel système de numération est utilisé. Ainsi, le nombre représenté en binaire par "101" (c'est-à-dire le nombre 5) sera noté :

• soit 101₂
• soit 101²
• et il y a d'autres notations existantes...

Le nombre représenté en décimal par "101" (donc cent un) peut être noté 101₁₀ ou tout simplement 101 puisque le système décimal est notre système habituel (sauf dans un exercice sur les nombres en binaire).

Ainsi nous pouvons écrire : 101₂ = 5₁₀.

Exercice

Exercice 3 de la fiche d'exercices.

Conversions binaire ⇆ décimal

Très bien, vous avez réussi précédemment à convertir quelques nombres entiers en binaire mais cela demande un peu de réflexion et de temps.

Nous allons maintenant chercher :

• des méthodes ou algorithmes permettant de convertir dans un sens et dans l'autre de façon mécanique ;
• une fois ces algorithmes obtenus, il sera possible de les traduire dans un langage de programmation (par exemple Python).

Pour comprendre comment faire ces conversions, commençons par comprendre comment fonctionne notre bonne vieille écriture décimale, à l'aide d'un exemple :

275 = 2 × 100 + 7 × 10 + 5 × 1 = 2 × 10² + 7 × 10¹ + 5 × 10⁰.

Vous le voyez, les chiffres 2, 7 et 5 du nombre 275 sont en fait des coefficients de puissances de 10 (décroissantes de la gauche vers la droite).

Conversions binaire → décimal

En binaire, le principe sera le même, mais avec des puissances de 2, ainsi le nombre écrit en binaire sous la forme 10010 est égal à :

10010 = 1 × 2⁴ + 0 × 2³ + 0× 2² + 1× 2¹ + 0× 2⁰ = 16 + 2 = 18 en notation décimale.

Exercice

1. Écrivez sous la forme décimale les "nombres binaires" suivants :
   A = 01101110
   B = 10010001
2. Que donne A + B ?
3. Par quel calcul direct aurions-nous pu passer directement de la forme décimale de A à celle de B ?

Conversions décimal → binaire

Convertissons le nombre 23 en binaire.

Première méthode : en utilisant les puissances de 2

• je cherche la plus grande puissance de 2 contenue dans 23 (ou "inférieure ou égale à 23") ; pour cela je liste les premières puissances : 1 ; 2 ; 4 ; 8 ; 16 ; 32 donc je m'arrête à 16 (2 puissance 4 donc il faudra donc 5 bits), je la retire de 23 : 23 - 16 = 7
• je recommence avec 7 : la plus grande puissance de 2 contenue dans 7 est 4, je la retire de 7 : 7 - 4 = 3
• je continue ainsi jusqu'à ce qu'il ne reste plus rien : 3 contient 2, il reste 3 - 2 = 1 puis 1 contient 1 et 1 - 1 = 0.

Conclusion : \(23 = 16+ 4+2+1 = 1\times2^4 + 0\times 2^3+ 1\times 2^2+1\times 2^1+1\times 2^0 = 10111_2\).

Exercice

Convertissez le nombre 56 en binaire.

Deuxième méthode : par divisions entières par 2

Divisons le nombre 42 par 2 autant de fois que possible :

\(42 = 2 \times 21 + 0 \qquad \qquad 21 = 2 \times 10 + 1 \qquad \qquad 10 = 2 \times 5 + 0\)

\(5 = 2 \times 2 + 1\qquad \qquad 2 = 2 \times 1 + 0\qquad \qquad 1 = 2 \times 0 + 1\)

nous nous arrêtons dès que la division entière donne 0 et nous lisons les restes (qui sont forcément des 0 et des 1) de la fin vers le début : 42 = 101010₂.

Il est possible de présenter ces calculs en posant les divisions de la façon suivante :

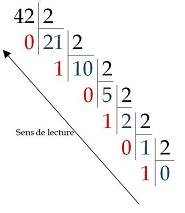(source)

Exercice

1. Convertissez le nombre 56 en binaire avec cette deuxième méthode.
2. Exercice 4 de la fiche d'exercices.

Une vidéo

Si vous n'avez pas tout compris, vous pouvez voir cette vidéo.

L'hexadécimal (ou base 16)

Présentation

L'hexadécimal est un système de numération assez utilisé en informatique. Au lieu d'utiliser des puissances de 10 (comme en décimal) ou des puissances de 2 (comme en binaire), nous utilisons des puissances de 16.

Certains auront remarqué qu'il faut disposer de 16 chiffres alors que nous n'en connaissons que 10 (les chiffres indiens, de 0 à 9) ! Plutôt que d'inventer de nouveaux chiffres, nous utiliserons les premières lettres de l'alphabet, ce qui donne les 16 "chiffres" suivants : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

Tableau de correspondance :

décimal	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
hexadécimal	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

Ainsi C₁₆ = 12 ; 15 = F₁₆ ; 23 = 16 + 7 = 1 × 16¹ + 7 × 16⁰ = 17₁₆.

En hexadécimal, le plus grand nombre que l'on peut écrire avec 2 "chiffres" est :
FF₁₆ = 15 × 16¹ + 15 × 16⁰ = 255 = 16² - 1.
Pour écrire ce même nombre en binaire, il faut 8 bits car 255 = 2⁸ - 1 = 11111111₂.

En fait, deux chiffres hexadécimaux permettent de décrire un octet.

Exercice

Les ordinateurs communiquent entre eux via des cartes réseaux. Chaque carte a un code qui l'identifie de façon unique, appelé adresse MAC.

Cherchez sur Internet comment afficher l'adresse MAC de la carte réseau de votre PC puis affichez-là. Quel est son format ?

Conversions hexadécimal ⇆ décimal

Conversions hexadécimal → décimal

Il suffit d'utiliser les puissances de 16, par exemple :

B5E43₁₆ = 11 × 16⁴+ 5 × 16³ + 14 × 16² + 4 × 16¹ + 3 × 16⁰ = 745027.

Exercice

1. Convertissez le nombre 8AF4₁₆ en décimal.
2. Exercice 5, question 1°) de la fiche.

Conversions décimal → hexadécimal

Nous utilisons la technique des divisions successives, cette fois-ci par 16.
Par exemple, convertissons 380 en hexadécimal :
380 = 16 × 23 + 12
23 = 16 × 1 + 7
1 = 16 × 0 + 1
et nous lisons les restes de la fin vers le début ; comme 12 se note C, cela donne : 380 = 17C₁₆

Exercice

1. Convertissez le nombre 937756 en hexadécimal.
2. Exercice 5, questions 2°) et 3°) de la fiche.

Réponse (pour 937756)

E4F1C

Conversions hexadécimal ⇆ binaire

Conversions hexadécimal → binaire

Il suffit de convertir chacun des chiffres hexadécimal en un mot de 4 bits.

Exemple : conversion en binaire du nombre hexadécimal B3E8A :

• B correspond à 11 en décimal donc 8 + 2 + 1 ce qui donne 1011 en binaire ;
• 3 correspond à 3 en décimal donc 2 + 1 ce qui donne 0011 en binaire ;
• E correspond à 14 en décimal donc 8 + 4 + 2 ce qui donne 1110 en binaire ;
• 8 correspond à 8 en décimal donc 1000 en binaire ;
• A correspond à 10 en décimal donc 8 + 2 ce qui donne 1010 en binaire ; donc

B3E8A₁₆ = 1011 0011 1110 1000 1010₂.

Exercice

1. Convertissez le nombre CE7F₁₆ en binaire.
2. Exercice 6, question 1°) de la fiche.

Conversions binaire → hexadécimal

Il suffit de :

• regrouper les bits par paquets de 4 (s'il faut, ajouter des zéros à gauche) ;
• convertir chaque paquet en un chiffre hexadécimal.

Exemple : le mot binaire 101110 donne deux groupes : 0010 et 1110, qui correspondent aux nombres 2 et 14 donc aux "chiffres" 2 et E donc

101110₂ = 2E₁₆.

Exercice

1. Convertissez le nombre 1101101110₂ en hexadécimal.
2. Exercice 6, question 2°) de la fiche.

Autres bases

Il est possible de prendre n'importe quelle base entière b (sauf b = 0 et b = 1, je vous laisse y penser).

Citons par exemple deux bases parfois utilisées :

• la base 8 (écriture octale) : le "mot" de 3 chiffres 173 en octal représente le nombre :

173₈ = 1 × 8² + 7 × 8¹ + 3 × 8⁰ = 64 + 56 + 3 = 123₁₀.

• la base 60 pour les heures : 4 heures 27 minutes et 51 secondes correspondent à :

4 × 60² + 27 × 60¹ + 51 × 60⁰ = 14538 secondes.

Il y a d'autres systèmes de numération mais ils sont moins utilisés, comme le codage de Fibonaci.

Utilisation de Python

Exercice

Lisez attentivement le contenu de cette page.

À retenir

• pour écrire un nombre en binaire, le préfixer avec 0b ;
• pour écrire un nombre en hexadécimal, le préfixer avec 0x ;
• pour obtenir l'écriture décimale d'un nombre, je peux aussi utiliser la fonction int(), soit avec un argument (le nombre préfixé avec 0b ou 0x) soit avec deux arguments (le nombre et sa base actuelle) ;
• pour obtenir l'écriture binaire d'un nombre, utiliser la fonction bin() ;
• pour obtenir l'écriture binaire d'un nombre, utiliser la fonction hex().

Exercice

En utilisant la console Python ci-dessous, complétez ce tableau :

Binaire		10011100
Hexadécimal	8F3A
Décimal			1429

>>>