
On reproche parfois aux mathématiciens de vouloir compliquer les choses en n'acceptant pas ce qui semble évident !
Nous verrons que bien que l'intuition soit précieuse dans certains cas, on ne peut arriver à une vérité sans une dose de rigueur et de mathématiques.
Ça y est, vous vous êtes décidé à vous mettre à courir (il paraît que c'est bon pour la santé).
Vous partez donc pour une course : pendant la moitié de celle-ci vous avez une vitesse moyenne de 20 km/h, mais, par manque d'entraînement, votre vitesse chute à 10 km/h pendant la seconde moitié de la course...
Quelle est donc votre vitesse moyenne sur l'ensemble de la course ? Facile, c'est logiquement 15 km/h !
Eh bien, pas du tout ! La vitesse moyenne est d'environ 13,3 km/h !!!
Observons le cas où vous avez couru 40 km :
Pour ceux qui aiment les maths, regardons ce qui se passe pour une distance parcourue quelconque.
La vitesse moyenne est la distance divisée par le temps : \[v=\dfrac{d}{t}\] on en déduit que \[t=\dfrac{d}{v}\] Appelons d la longueur de la moitié du trajet.
Le temps nécessaire pour courir la moitié du trajet est alors \(t_1=\dfrac{d}{20}\).
Le temps nécessaire pour courir la seconde moitié du trajet est \(t_2=\dfrac{d}{10}\).
La vitesse moyenne pour l'ensemble de la course est donc : \[ v=\dfrac{2d}{t_1+t_2} = \dfrac{2d}{\frac{d}{20}+\frac{d}{10}} = \dfrac{2}{\frac{1}{20}+\frac{1}{10}} = \dfrac{2}{\frac{1}{20}+\frac{2}{20}} = \dfrac{2}{\frac{3}{20}} = 2\times \dfrac{20}{3} =\dfrac{40}{3} \simeq 13,3 \text{ km/h}. \]
Il est possible de déplacer un élève d'une classe à une autre et d'augmenter ainsi la moyenne des deux classes !
En voici un exemple (on a réduit la taille des classes pour simplifier) :
On déplace l'élève qui a 10 de la classe 1 vers la classe 2, ce qui donne donc :
Les moyennes des deux classes ont donc augmenté !!
Remarque : une fois cet exemple donné, ce phénomène perd son côté contre-intuituif. Ce n'est pas le cas de ceux qui suivent, qui le restent malgré les exemples...
Soient deux sportifs, disons Bart et Lisa. On compare leur performance sportive pendant deux années.
Il est possible que Bart ait de meilleurs taux de réussite pendant chacune des deux années mais que Lisa l'emporte sur les deux années mélangées !
Par exemple :
| Année 1 | Année 2 | Sur les deux années | |
|---|---|---|---|
| Lisa | 60 % | 10 % | 55,45 % |
| Bart | 90 % | 30 % | 35,45 % |
| Bart l'emporte | Bart l'emporte | Lisa l'emporte ! |
Détaillons comme obtenir les pourcentages ci-dessus : la première année, Lisa gagne 60 matchs sur 100 et Bart en gagne 9 sur 10 ; la deuxième année Lisa gagne 1 match sur 10 et Bart 30 sur 100.
Au final, Lisa a gagné 61 matchs sur 110 et Bart seulement 39 sur 110 donc il est perdant !
| Année 1 | Année 2 | Total | |
|---|---|---|---|
| Lisa | 60/100 = 60 % | 1/10 = 10 % | 61/110 = 55,45 % |
| Bart | 9/10 = 90 % | 30/100 = 30 % | 39/110 = 35,45 % |
(source : article de wikipedia, où on trouvera un exemple issu d'un cas de traitement du cancer, également utilisé dans une vidéo sur la chaîne Science étonnante.)
Considérons un test de dépistage d'une maladie, qui fonctionne dans 99 % des cas, c'est-à-dire que :
Une personne passe le test et ce dernier est positif. Quelle est la probabilité que cette personne soit effectivement malade ? Beaucoup de gens répondront qu'il y a 90 % de "chances" qu'il soit bien malade. D'autres, plus méfiants, diront que la réponse n'est peut-être pas 90 % mais qu'elle doit être très élevée quand même...
En fait il n'en est rien !
Supposons que la population totale soit de 100 000 personnes et que la maladie touche une personne sur 1 000.

Alors :
La probabilité d'être effectivement malade lorsqu'on est dépisté malade dépend en fait fortement de la virulence de la maladie.
Ainsi, si la maladie touche 1 personne sur 100 000 alors la probabilité calculée précédemment descend à 0,1 % !
Finissons-en avec les pourcentages avec deux remarques/questions :
Comment savoir si deux nombres sont différents ? Par exemple 0,9 et 1 sont différents car il y a un écart entre les deux, à savoir 1 - 0,9 = 0,1
(on peut de même prouver que 2/3 et 5/7 sont différents car leur différence 2/3 - 5/7 vaut -1/21, ce qui est petit mais non nul).
Observons maintenant ce tableau :
| Nombre | 0,9 | 0,99 | 0,999 | 0,999999999 |
| Différence avec 1 | 0,1 | 0,01 | 0,001 | 0,000000001 |
Que se passe-t-il maintenant s'il y a une infinité de 9 ?
Supposons qu'il y ait une différence \(d\) entre 0,999... et 1. Alors :
\(d<0,1\) car 0,999... est plus proche de 1 que 0,9 ;
\(d< 0,001\) car 0,999... est plus proche de 1 que 0,999 ;
\(d < 0,000000001\) car 0,999... est plus proche de 1 que 0,999999999 ;
etc.
Conclusion : \(d\) est aussi petit que l'on veut donc \(d = 0\).
Puisqu'il n'y a pas de différence entre 0,999... et 1 on peut conclure que 0,999... = 1.
Pas convaincu ? Voici un autre raisonnement : \[1/3 = 0,3333....\] donc \[3 \times (1/3) = 3 \times 0,3333.... \] d'où \[1 = 0,9999...\]
Ce paradoxe est inspiré d'un jeu télévisé américain animé par Monty Hall.
Le principe est le suivant : vous faîtes face à trois portes fermées ; derrière deux d'entre elles se trouvent une chèvre et derrière la troisième se trouve par exemple une voiture de sport, que vous remporterez si vous choisissez la bonne porte.
(source de l'image : Wikipédia)
Ce choix se fait en trois temps :
- vous choisissez une porte, par exemple celle de gauche (mais cette porte reste fermée) ;
- l'animateur, qui sait ce qu'il y a derrière chaque porte, ouvre une des deux autres portes, par exemple celle du centre, derrière laquelle se trouve une chèvre ;
- vous avez maintenant le choix : soit vous conservez la porte que vous aviez choisie au départ (celle de gauche), soit vous choisissez l'autre porte fermée (celle de droite dans mon exemple).
Bien évidemment, cela ne devrait rien changer : après tout il y a autant de chances que la voiture soit derrière la porte de gauche que de chances qu'elle soit derrière celle de droite...
Et pourtant, l'expérience montre qu'on a intérêt à toujours changer de porte pour augmenter ses chances de réussite !!
Pour faire court, la probabilité que vous ayez choisi la bonne porte est de 1 chance sur 3 et donc il y a deux chances sur 3 que la bonne porte soit parmi les deux autres ; par conséquent il y a 2 chances sur 3 que la porte restante soit la bonne et seulement 1 chance sur 3 que votre premier choix soit le bon : il faut changer de porte au deuxième choix. Ce résultat peut d'ailleurs être vérifié par simulation informatique.
Vous trouverez un raisonnement expliquant davantage ceci dans cette vidéo.
Quelle est la probabilité que deux personnes sur un terrain de football (22 joueurs + 1 arbitre) aient le même jour d'anniversaire (par exemple, deux des personnes sont nées un 15 mars) ?
1 chance sur 100 ? 1 chance sur 1000 ?
Vous êtes très loin du compte en fait... Il y a plus d'une chance sur deux (plus de 50 % de chance) que cela se produise !
Vous trouverez des explications sur cette page ou sur celle-ci.
Dans le même registre, vous trouverez sur cette page un graphique montrant, par exemple, qu'il y a plus de chance de gagner à "Qui veut gagner des millions ?" en répondant au hasard que de réunir 120 personnes choisies au hasard sans qu'aucune date d'anniversaire commune ne se présente.
Supposons que vous disposiez d'un terrain agricole, vous devriez alors le clôturer pour éviter que des animaux viennent manger toutes vos laitues.
Admettons dans un premier temps que votre terrain soit carré :

on constate dans ce cas, et cela se démontre assez facilement, que plus la longueur de clôture est grande, plus le terrain délimité est grand.
Vérifions que la même chose s'applique à un terrain circulaire (les valeurs sont ici arrondies) :

Là aussi, plus la clôture est grande, plus le terrain est grand.
Une première question se pose naturellement : est-ce-que la surface d'un terrain de forme variable augmente systématiquement quand la longueur de la clotûre augmente ?
On a envie de dire oui mais ce n'est pas le cas et il suffit de regarder les figures ci-dessus : le disque de droite a une clôture plus petite que celle du carré de droite mais le terrain est pourtant plus grand.
On en déduit une deuxième question : si je dispose de, par exemple, 40 mètres de clotûre, quel doit la forme de mon terrain pour que sa surface soit maximale ?
La réponse à ce problème (appelé problème des isopérimètres) est simple : il faut que le terrain soit circulaire.
(voici un document assez complet sur ce sujet).
Finissons par un dernier questionnement : si la longueur de la clôture devient très très grande alors mon terrain devient-il très très grand ?
La réponse semble être oui de toute évidence... Mais observez la figure suivante, appelée flocon de Von Koch (c'est une fractale ; source de l'image : Wikipédia) :

On démontre que la longueur de cette courbe augmente à chaque étape et peut être rendue aussi grande que l'on veut.
Cependant, la surface du terrain qui est délimité par cette "clôture" n'est pas infinie car elle est inférieure à celle du carré qui entoure la courbe !
Pour aller plus loin, consultez par exemple ces pages sur les fractales.
Dans le prolongement du paragraphe précédent, voyons maintenant ce qui se passe avec des solides de dimension 3 : un volume fini peut-il correspondre à une surface infinie ? un volume infini peut-il correspondre à une surface finie ?
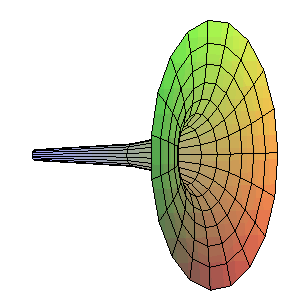
Remarquons pour finir qu'il existe un solide, en forme de vase, de volume fini mais qui peut contenir un volume infini : le "vase de Sluse".
Que se passe-t-il quand un ensemble A est contenu dans un autre ensemble B ?

On peut alors dire que A est plus "petit" que B mais qu'est-ce-que cela veut dire ?
Tout simplement que A contient moins d'éléments que B : dans la figure ci-dessus, A contient 4 éléments (on dit que le cardinal de A est 4) tandis que B en contient 13 (son cardinal est 13).
Ceci semble évident mais en fait ce n'est pas le cas : un ensemble A peut être contenu dans un ensemble B et avoir autant d'éléments que B !
Par exemple, il y a autant de nombre entre 0 et 1 que de nombres tout court...
Alors, oui, le cardinal est ici infini mais saviez-vous :
Plutôt que ré-inventer la roue, je vous invite à consulter des vidéos très bien faites sur la chaîne Science étonnante, El Jj, Science4all. et la vidéo How big is infinity, très bien illustrée (avec des sous-titres en français)
Observez la figure ci-dessous (cliquez sur le bouton lecture ou déplacez à la souris le curseur n) :
Explication : il faut bien comprendre qu'il n'y a pas de "fin". A n'importe quelle étape, la ligne brisée reste une ligne brisée et, bien que la taille des "marches" devienne très petite, il y en a de plus en plus ce qui permet à la ligne brisée de conserver une longueur constante (\(2\times1=4\times\frac{1}{2}=8\times\frac{1}{4}=\dots=2^{100}\times\frac{1}{2^{99}}=\dots=2\)).
Par ailleurs, un argument pour dire que la ligne brisée ne devient pas le segment "à la limite" consisterait à remarquer que celle-ci comporterait une infinité dénombrable de marches alors que le segment a un infini indénombrable, voir le paragraphe précédent sur les ensembles de Cantor (cet argument serait dû à Albert Jacquard dans L'équation du nénuphar).
Les rectangles existent-ils ? Cette question semble idiote : il y a des cours de mathématiques entiers sur les rectangles, c'est donc qu'ils doivent exister ! En fait la réponse et oui et... non, et d'ailleurs plutôt non que oui !
Commençons par parler des rectangles dans la réalité : les rectangles n'existent pas !
Si je veux dessiner un rectangle, j'utilise une équerre et je trace successivement quatre côtés, avec un angle droit entre deux côtés consécutifs ; cependant, il y a forcément une imprécision dans le tracé, aucun des angles droits ne fera exactement 90° (un des angles pourra faire par exemple 89,948541...°) de sorte qu'on ne peut pas dessiner un vrai rectangle.
De même, un segment mathématique n'existe pas dans la réalité car tout objet a une épaisseur (par exemple celle du crayon quand vous tracez ce segment).
Les mathématiques décrivent donc des objets idéaux, qui n'existent pas ni dans la nature, ni dans la création humaine (qui reste limitée par la nature).
OK, maintenant posons la question plus précise suivante : existe-t-il des rectangles dans le monde idéal des mathématiques ?
Après tout, ce n'est pas si évident : qu'est-ce-qui me prouve qu'en tournant trois fois à angle droit, je finirai par revenir sur la direction de départ avec un angle droit ?

En fait, les rectangles existent ... ou n'existent pas !
|
Pour comprendre cela, il faut savoir que l'existence des rectangles repose entre autres sur le 5ième postulat d'Euclide : "Il existe une droite unique parallèle à une droite donnée et passant par un point extérieur à cette droite."
(en vérité la formulation d'Euclide est plus compliquée que celle-là).
Euclide est un mathématicien grec qui a recensé, vers - 300 avant JC, toutes les connaissances mathématiques (donc géométriques à l'époque) et a essayé de construire un édifice solide où tous les théorèmes se déduiraient de quelques définitions et postulats (ou axiomes) qu'on ne peut pas démontrer. Les quatre premiers postulats sont très simples (par exemple, le premier postulat est "par deux points, il ne passe qu'une seule droite") mais le 5ième l'est beaucoup moins ; pendant environ 2000 ans, les mathématiciens le considérait vrai mais se sont demandés si on ne pourrait pas se débarasser de ce 5ième postulat en le déduisant des quatre premiers. |
(image issue de Wikipedia) |
On a donc fini par essayer de voir ce qui se passerait si ce postulat était faux, afin d'arriver à une absurdité (ce qui prouverait que le postulat est vrai) mais aucune incohérence n'est apparue et, au 19ième siècle, trois mathématiciens (Gauss, Bolyai et Lobatchevski) ont ainsi pu créer de nouvelles géométries, dites non-euclidiennes, dans lesquelles le 5ième postulat est faux !
Par exemple, en géométrie hyperbolique :
"Il existe une infinité de droites parallèles à une droite donnée et passant par un point extérieur à cette droite."

sur cette figure, les trois droites d1, d2 et d3 sont parallèles à D et passent par M (source de l'image Wikipédia)
De même, dans ces géométries non euclidiennes :
En fait, la géométrie euclidienne (la géométrie de collège) est celle d'un espace plat, comme par exemple, une feuille de papier ou le tableau du professeur.
Mais alors, ces nouvelles géométries décrivent-elles la réalité ou ne sont-elles qu'une pure invention abstraite ?
La Terre n'est pas plate, comme chacun le sait, donc la géométrie euclidienne ne s'applique pas.
Cependant, à l'échelle humaine, on ne perçoit pas la courbure de la Terre et on peut quand même utiliser cette géométrie, qui fonctionne bien, mais de façon approximative.
(de même, dans la théorie de la relativité générale d'Einstein, l'espace est courbé par la présence de masses et d'énergie donc il n'y a pas vraiment d'espace plat...)
Pour finir, quelques vidéos sur ce sujet :
|
Aristote (4ième siècle avant JC) a introduit la notion de tiers-exclus : soit un énoncé est vrai, soit il ne l'est pas (il n'y a pas de troisième cas possible). En effet, dans la vie courante, on constate la validité apparente de cette idée : soit mon prof de maths est excellent, soit il n'est pas excellent ; soit je parle parfaitement le chinois, soit je ne parle pas parfaitement le chinois etc. En mathématiques, pour qu'un énoncé puisse être considéré comme vrai de façon certaine, on demande une démonstration de cet énoncé, c'est-à-dire un enchaînement de raisonnements logiques partant d'hypothèses connues et arrivant à cet énoncé. |
(Wikipedia) |
Confrontés à toutes sortes de phénomènes contradictoires ou contre-intuitifs, les mathématiciens ont eu le besoin d'assoir leurs théories sur des bases solides en construisant des systèmes d'axiomes (des énoncés simples et évidents) dont on pourrait déduire tous les théorèmes existants et à venir.
Malheureusement pour eux, il restera toujours des énoncés qu'on ne pourra démontrer ni refuter et, en fait, on peut choisir s'ils sont vrais ou faux sans que cela ne pose de problème de cohérence !
On dit que ces énoncés sont indécidables.
Ainsi :
Parlons un peu plus de ces deux derniers énoncés.

(source de l'image : Wikipédia)
Axiome du choix : "étant donnée une collection (éventuellement infinie) d'ensembles non vides, on peut choisir un élément dans chacun de ces ensembles."
On comprend que cet énoncé soit appelé axiome, tellement il paraît évident ! Cependant, on ne peut pas le démontrer, ni démontrer qu'il est faux (Gödel et Cohen) à partir des axiomes ZF et, plus génant, si on considère qu'il est vrai alors on est amené à des conclusions assez absurdes, telles que le paradoxe de Banach-Tarski, qui dit qu'on peut découper une sphère en un nombre fini de morceaux et ré-assembler ces morceaux pour former... deux sphères identiques à la première !!! On comprend que certains mathématiciens évitent, quand c'est possible, d'utiliser l'axiome du choix...
Si vous avez regardé les vidéos présentes dans le paragraphe sur les ensembles de Cantor, vous savez maintenant qu'il existe une infinité d'infinis !
|
Si l'axiome du choix est accepté alors :
Cantor a prouvé (les preuves sont simples) que les ensembles ℕ, ℤ, ⅅ et ℚ ont le même cardinal ℵ0 et que ℝ a un cardinal plus grand que ℵ0.
Il a alors supposé qu'il n'existe pas d'infini "plus grand" que celui des entiers mais "plus petit" que celui des réels, autrement dit que ℵ1 est le cardinal de ℝ mais, malgré ses efforts, il n'a pas réussi à le prouver. C'est ce qu'on appelle l'hypothèse du continu (HC pour les intimes) : Il n'y pas d'infini plus grand que le cardinal de ℕ et plus petit que le cardinal de ℝ (la figure ci-contre représente un cas où cette hypothèse serait fausse).
Gödel a prouvé qu'on ne peut pas trouver de démonstration du contraire de l'HC mais Cohen a plus tard prouvé qu'on ne peut pas non plus démontrer l'HC donc l'HC est un indécidable dans l'axiomatique ZFC (Zermelo Fraenkel + Axiome du choix) : on ne peut pas affirmer qu'il existe ou qu'il n'existe d'infini intermédiaire entre celui de ℕ et celui de ℝ.
Quelques excellentes vidéos pour finir :
|
 |
Et un bon article de Jean Paul Delahaye sur l'indécidabilité.
Remarque : il y a d'autres énoncés indécidables, tels que :
On le sait depuis l'antiquité, tout nombre peut se décomposer comme produit de nombres premiers. Bien, mais combien de facteurs premiers apparaissent dans la décomposition ?
Par exemple :
\(120 = 2\times 2\times2\times3\times5\) donc la décomposition de 120 a 5 facteurs premiers ;
\(216 = 2\times 2\times2\times3\times3\times 3\) donc la décomposition de 216 a 6 facteurs premiers.
On le voit, le nombre de facteurs premiers est parfois pair, parfois impair. Quel est le cas le plus fréquent ?
Vous pouvez tester le script à cette adresse pour essayer de répondre à cette question. On trouve par exemple que :
On le voit : il y a plus de décompositions avec un nombre impair de facteurs premiers que de décompositions avec un nombre pair de facteurs premiers.
On peut donc supposer que cela reste toujours vrai, cette affirmation est appelée la conjecture de Pólya, qui l'a énoncée en 1919.
Cette conjecture a été testée et vérifiée pour de grands nombres et semblait donc vraie.
Cependant, on a trouvé (à partir de 1958) des contre-exemples à cette conjecture et le plus petit d'entre eux est 906 150 257 (on comprend que la conjecture de Pólya ait pu être considérée vraie pendant un certain temps) !
La répartition des nombres premiers est une des questions les plus complexes, reliée à beaucoup de problèmes non résolus.
On sait qu'il y a une infinité de nombres premiers mais qu'ils deviennent de plus en plus rares.
Par exemple :
Si on note \(\pi(n)\) (rien à voir avec le nombre \(\pi\)) le nombre de nombres premiers inférieurs ou égaux à \(n\) alors \(\pi(100)=25\) ; \(\pi(1000)=168\) et \(\pi(10000)=1229\).
Des mathématiciens ont prouvé que \(\pi(n)\simeq L_i(n)\) où \(L_i\) est la fonction d'écart logarithmique intégral, définie par \(L_i(n)\simeq \displaystyle\int_{2}^{n}\dfrac{1}{\ln x}dx\).
Le graphique ci-dessous donne une représentation graphique des fonctions \(\pi\) et \(L_i\), pour des entiers jusqu'à 16000 (fichier Geogebra).

Effectivement, les deux fonctions sont proches mais on constate de plus que la courbe de \(\pi\) reste en dessous de celle de \(L_i\), d'où la conjecture :
\[\pi(n)\le L_i(n)\ \text{pour tout entier }n\]qui, puisqu'elle est vraie pour au moins 16000 valeurs (et bien plus en fait), devrait être toujours vraie...
Et pourtant, cette conjecture est fausse !
Littlewood a démontré en 1914 qu'il existe une infinité de valeurs de \(n\) pour lesquelles \(\pi(n)>L_i(n)\), le problème est qu'on n'en a pas encore trouvé.
Tout ce que l'on sait, depuis 2000, c'est que le plus petit nombre \(n\) vérifiant \(\pi(n)>L_i(n)\) est inférieur à environ \(1,39822\times 10^{316}\), c'est-à-dire
13982200000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 !!!
(Article de Wikipédia sur ce nombre).
La conjecture de Hardy-Littlewood (plus de détails ici) a été vérifiée pour de très grands nombres mais les mathématiciens pensent qu'elle est pourtant fausse et qu'un contre-exemple doit exister entre 1,5 × 10174 et 2,2 × 101198 (source : Wikipédia) !!
Là encore, je vous invite à consulter cette vidéo de Science4all qui présente quelques courbes et volumes surprenants.