(source : sigmaths)
Le triangle "dit de Pascal" a été étudié de façon détaillée par Blaise Pascal mais sa découverte remonte aux mathématiciens persans (Al-Karaji, vers le Xème siècle).
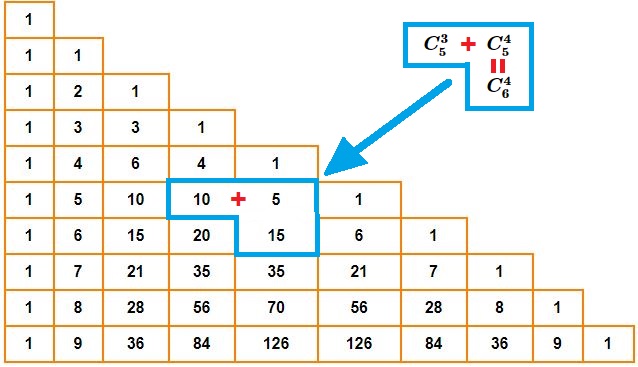
En voici une représentation :

Chaque valeur s'obtient en ajoutant la valeur au dessus et celle qui est au dessus et à gauche.
Le triangle de Pascal intervient dans les probabilités ainsi que dans les développements d'expressions de la forme \((a+b)^n\).
Ecrivez une fonction `tri_Pascal` en Python qui renvoie un triangle de Pascal sous forme d'une liste de listes.
Par exemple :
>>> tri_Pascal(3) [[1], [1,1], [1, 2, 1], [1, 3, 3, 1]]
Ecrivez une fonction `affiche_tri_Pascal` en Python qui affiche un triangle de Pascal (utilisez la fonction `tri_Pascal`) :
Par exemple :
>>> affiche_tri_Pascal(3) 1 1 1 1 2 1 1 3 3 1
Voici les développements de quelques expressions de la forme \((a+b)^n\) :
\[(a+b)^0 = 1\] \[(a+b)^1 = a+b = 1a^1+1b^1\] \[(a+b)^2 = a^2+2ab+b^2 = 1a^2+2a^1b^1+1b^2\] \[(a+b)^3 = a^3+3a^2b+3ab^2+b^3 = 1a^3+3a^2b^1+3a^1b^2+1b^3\] \[(a+b)^4 = a^4+4a^3b+6a^2b^2+4ab^3+b^4 = 1a^4+4a^3b^1+6a^2b^2+4a^1b^3+1b^4\]Vous le voyez, la puissance de \(a\) diminue tandis que celle de \(b\) augmente et les coefficients sont les nombres d'une ligne du triangle de Pascal.
Il existe une formule générale, appelée formule du binôme de Newton.
Ecrivez une fonction `binome_Newton` en Python qui affiche le développement de \((a+b)^n\) en fonction de \(n\) :
Par exemple :
>>> binome_Newton(5) 1 a^5 b^0 + 5 a^4 b^1 + 10 a^3 b^2 + 10 a^2 b^3 + 5 a^1 b^4 + 1 a^0 b^5puis améliorez votre fonction pour avoir :
>>> binome_Newton(5) a^5 + 5 a^4 b + 10 a^3 b^2 + 10 a^2 b^3 + 5 a b^4 + b^5
Petites variantes : écrivez des fonctions qui donnent :
-- le développement de \((a-b)^n\)
-- le développement de \((x+2)^n\)
Par exemple, pour la deuxième fonction :
>>> dev(5) x^5 + 10 x^4 + 40 x^3 + 80 x^2 + 80 x + 32