Le voyageur de commerce
Un voyageur de commerce doit parcourir une certaine liste de villes (un seul passage par ville) et il connaît les distances entre deux villes quelconques.
Comment doit-il s'organiser pour minimiser la distance qu'il doit parcourir ?
Exercice 4
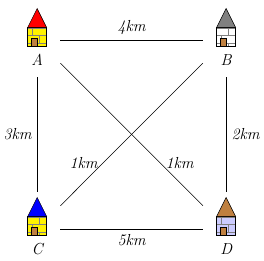
Le voyageur part de la ville A et doit finir en A après être passé une seule fois par chaque ville. Recherchez tous les trajets et donnez un trajet optimal.
Nombre de chemins possibles (recherche exhaustive)⚓︎
Supposons qu'il y ait n villes à visiter en tout. Laissons de côté la ville de départ (et d'arrivée), il reste n − 1 villes.
Le voyageur doit choisir :
- la première ville à visiter : n − 1 choix ;
- la deuxième ville à visiter : n − 2 choix ;
- la troisième ville à visiter : n − 3 choix ;
- etc.
- la dernière ville à visiter : 1 choix
soit \((n − 1) \times (n − 2) \times (n − 3) \times \dots \times 2 \times 1\) choix.
En mathématiques, ce nombre est noté \((n − 1)!\) (factorielle de \(n − 1\)).
Cependant, dans ce calcul, la moitié des trajets est inutile pour nous, par exemple Lille-Paris-Lyon-Lille revient à Lille-Lyon-Paris-Lille en terme de distance totale.
Bref, le nombre de chemins possibles est au final \(\dfrac{(n − 1)!}{2}\).
Calculons ce nombre de chemins dans quelques cas :
| Nombre de villes n | 5 | 10 | 20 | 100 |
| Nombre de chemins (n − 1)!/2 | 12 | 181440 | 6,0823 × 1016 | 4,6663 × 10155 |
Ainsi, ce problème donne encore plus de cas à envisager que celui du sac à dos. A titre de comparaison, pour n = 10 :
- 210 = 1024 combinaisons d'objets pour le sac à dos ;
- 9!/2 = 181440 chemins pour le voyageur de commerce.
La recherche exhaustive semble donc inenvisageable, par exemple, pour 71 villes, le nombre de chemins est supérieur à 5 × 1080 qui est de l'ordre du nombre d'atomes dans l'univers connu !
Encore plus étonnant, si le calcul d'un chemin prend une microseconde, alors voici les temps de calculs de tous les chemins :
- pour 10 villes : 181 440 microsecondes = 0,18 seconde ;
- pour 15 villes : 43 589 145 600 microsecondes = 12 heures environ ;
- pour 20 villes : 6 × 1016 microsecondes soit environ 1 901 années ;
- pour 25 villes : le temps de calcul dépasse l'âge de l'Univers...
Le voyageur va donc devoir se contenter d'un algorithme glouton qui lui donnera un chemin convenable mais pas forcément optimal.
Méthode gloutonne⚓︎
Exercice 5
- Quelle est la stratégie gloutonne qui vous paraît la plus adaptée (quel est le critère de choix de la prochaine ville du chemin) ?
-
Appliquez cette stratégie à cette configuration (le tableau donne les distances entre les villes) :
A B C D E F A 0 30 44,7 72,8 22,4 60 B 30 0 22,4 44,7 28,3 30 C 44,7 22,4 0 30 30 28,3 D 72,8 44,7 30 0 60 22,4 E 22,4 28,3 30 60 0 53,9 F 60 30 28,3 22,4 53,9 0 -
Donne-t-elle le chemin optimal ?
Aide
Voici une représentation graphique de la disposition de ces villes :

Exercice 6 : pour les plus rapides
Vous pouvez essayer de programmer un algorithme glouton pour le problème du voyageur de commerce (en entrée : une liste de villes et une liste de listes donnant les distances entre deux villes, en sortie : la liste des villes à parcourir dans l'ordre).